Coger con pinzas las estadísticas salariales

Doctor en Ciencias Económicas y consejero delegado de Inurrieta Consultoría Integral

La caída de los salarios es superior a la que muestra la estadística, porque debemos tener en cuenta que, tras la destrucción de trabajos temporales ocupados por jóvenes, el empleo que queda es el más cualificado y mejor pagado.

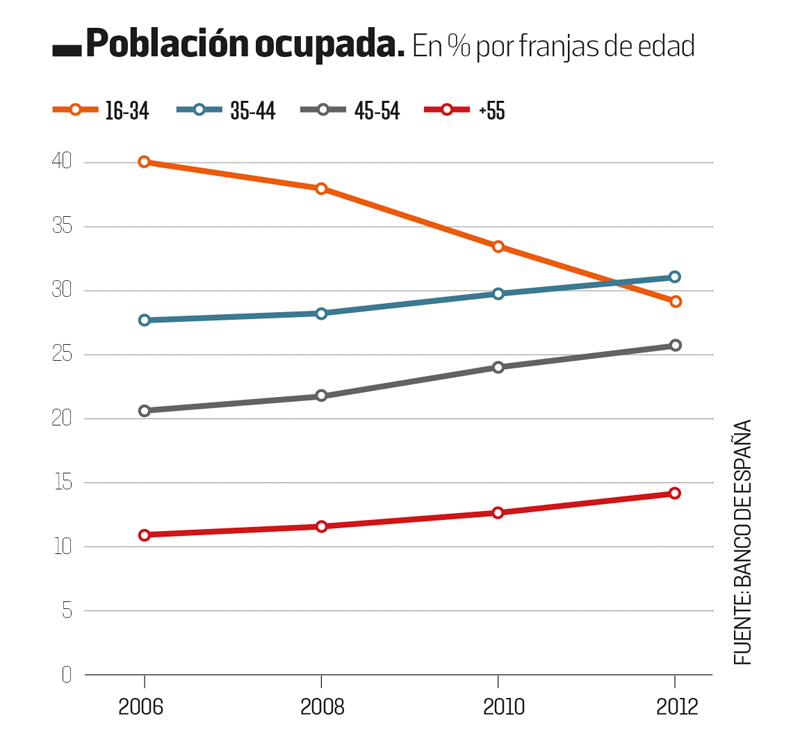
En un mercado laboral como el español, en el que los trabajadores entran y salen con una gran volatilidad, el análisis de los salarios de forma agregada presenta disfunciones relevantes cuando se quieren cuantificar. En particular, desde 2008, la enorme destrucción de empleo no cualificado y con escasa experiencia afecta al resultado agregado, ya que estos trabajadores cobran, de media, salarios inferiores.

Los cambios en la composición y la estructura del empleo en España han sido notables. La tendencia desde 2006 ha sido la de destruir el empleo temporal, menos cualificado y más joven. Este ha perdido nueve puntos de participación entre 2008 y 2012, mientras que los trabajadores extranjeros lo han hecho en dos puntos porcentuales. En materia de experiencia laboral, el salto de los trabajadores con más de tres años de permanencia en la empresa ha pasado del 60% al 73%. Ello demuestra que se han quedado los trabajadores más antiguos, más formados y, por tanto, más caros.

Con estas premisas, las estadísticas de salarios en agregado, como hace la Encuesta de Salarios que elabora el Instituto Nacional de Estadística (INE), pueden originar sesgos estadísticos significativos, algo esencial para llevar a cabo un diagnóstico correcto de la evolución salarial.

Para ello, es necesario tener información desagregada sobre salarios percibidos por los trabajadores en función de su categoría profesional, experiencia, edad o género. Esta información la proporciona la Muestra Continua de Vidas Laborales, a partir de datos de cotización a la Seguridad Social (hasta el año 2012). A partir de ahí, una vez filtrado el efecto de la composición del empleo, la estimación de la ecuación de salarios se realiza mediante una simple fórmula(1).

Los efectos observados en los salarios una vez descontados los efectos de composición del empleo son, en algunos casos, llamativos. A partir de 2006, las bases de cotización repuntaron levemente en el sector privado, tras años de estabilidad. A partir de ahí inician un período de moderación, con picos extraños, como el de 2009. Pero si analizamos los salarios reales netos del efecto de composición, la evolución es más lógica.

Con el inicio del proceso de destrucción de empleo, en 2008, la contribución de los efectos de composición aumentó de forma significativa y contribuyó con 1,3 puntos porcentuales cada año al incremento de las bases de cotización observado. Esto se resume en que el empleo que se ha quedado es el de mayor nivel de cualificación y el de un poder adquisitivo más elevado. Aun así, solo a partir de 2010 se observa una reducción notable de los salarios, que fue en 2012 del 2%, superior a lo que marca el dato del INE.

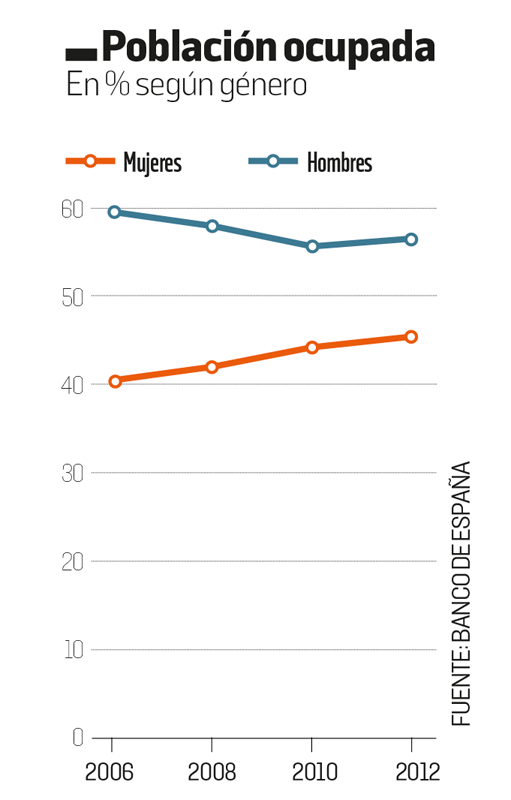Veamos ahora cuáles son los efectos que predominan entre todos los que componen el trabajo. El efecto de la edad, la experiencia y la cualificación tiene un impacto positivo sobre los salarios, al haber aumentado los grupos con mayor salario relativo. Durante los primeros años de la crisis, la experiencia tuvo un impacto mayor que la edad y reflejó la destrucción de empleo temporal. La cualificación media ha tenido una evolución más estable, aunque también destacó entre 2010 y 2012. La edad ha tenido menor influencia, aunque ha aumentado en los últimos años.

Concluyendo, los cambios en la composición del empleo han determinado la evolución de los salarios. En términos relativos, la destrucción de empleo se ha cebado con los jóvenes, trabajadores de menos cualificación y con poca experiencia. Por eso, y dado que el empleo que se ha quedado es de los grupos de mayor salario relativo, se ha observado que en los primeros años de la crisis los salarios parecían crecer, pero una vez descontado este efecto de composición, los salarios ya reflejan una caída significativa, mayor que la que muestran las estadísticas oficiales.

1. La fórmula es Wit = ft(Xit) + eit. La i  representa al individuo, w es el logaritmo del salario y X es un vector de características del individuo que influyen sobre el salario. La estimación de los efectos de la composición del empleo sobre el salario se obtendría manteniendo constantes las características y observar en el período t + 1 cómo sería el salario del mismo individuo.